

From the diagram above, it should be very easy to see which are which. And there is only one combination which affects all three parity bits. These will account for those data bits which affect two parity bits. There are three combination where two of the comparisons generate an error.

If you want to correct the parity bits you can do that merely by accepting your own generated parities.) If a channel coding scheme is employed at the transmitter, the detected data at the DSP output should be applied to a channel decoder unit to recover the. (You can choose to correct the parity bit, but I think that's pointless.
#Hamming circuit coder code
So this accounts for three more combinations, leaving only four remaining to consider. Design of Hamming Code Encoding and Decoding circuitthis video covers circuit of hamming code designed for 4 bit data word. There are exactly three possible cases where only one comparison generates an error. If only one, then it is a parity bit error. But if that's so, then only one of the comparisons will produce an error. It's possible that one of the parity bits is itself the error and that the data bits are just fine. But if the generated parities match up with the transmitted parities, then there is no single-bit error (this doesn't entirely exclude multi-bit errors.) So that accounts for one of the combinations, leaving seven to consider. There are eight possible combinations of these three comparison bits. This produces another set of three generated parity values, which can now be compared with the parity bits included in the 7-bit message. Upon receipt, a receiver performs the same function using generators \$P_1\$, \$P_2\$, and \$P_3\$ to replicate the work, applying them to the received 4 data bits. This generates 7 total bits out of 4 data bits. Department of Electrical Engineering Linkpings Universitet, SE-581 83 Linkping, Sweden.
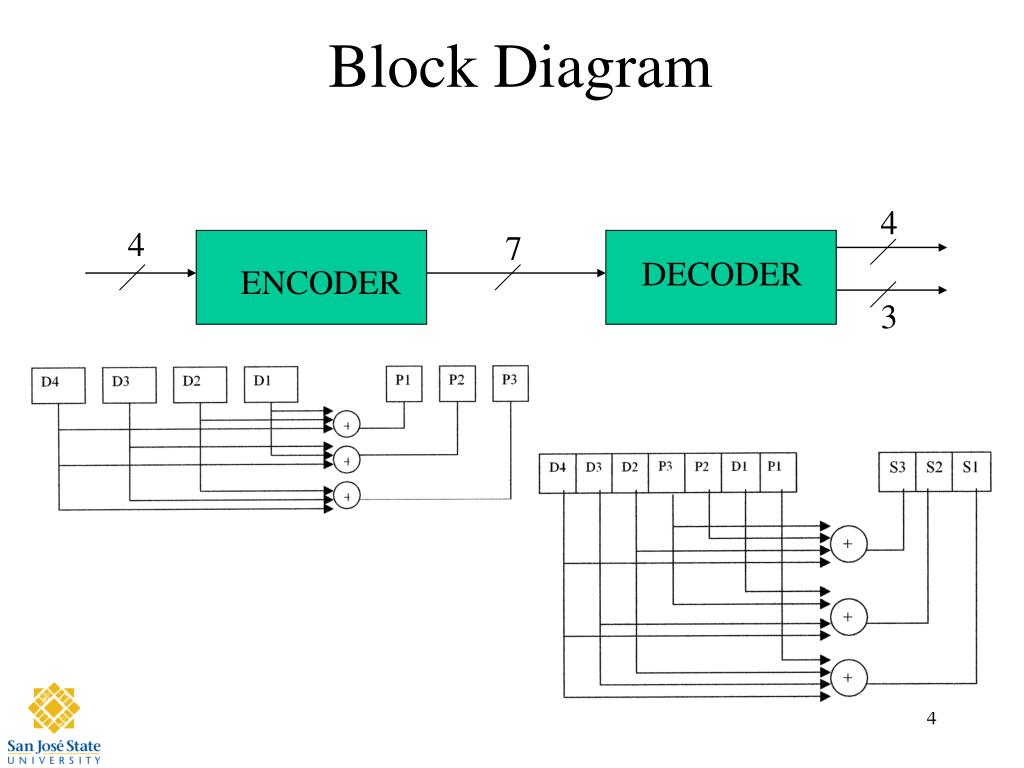
Doesn't really matter if this is odd or even parity generation, so long as the receiver of the message shares the method. CODING CIRCUITS FOR REDUCING HAMMING WEIGHT. The original generators, \$P_1\$, \$P_2\$, and \$P_3\$, will have produced their values as a result of generating parity for the values within their circle. This is just another way of writing your table, except more visual and quicker to navigate without holding things in your head while you read a row. This diagram makes things really easy to understand, I think:


 0 kommentar(er)
0 kommentar(er)
